入射電界の振幅5 電磁波の反射・透過・散乱 51 電磁界の境界条件 2つの異なる媒質の境界面においても電磁界はMaxwell の方程式で規定される物理的な条件を満足しなけ ればならない。これが電磁界の境界条件である。外部境界条件と重なるときはこちらが優先されます。 種類と境界条件名はユーザが設定できます。 外部境界条件 解析実行時にモデルの一番外側に設定されます。 外部境界条件の種類はユーザが選択できます。 境界条件は大きく3つに分けられます。Bの垂直成分が連続となる(Maxwellの境界条件)。ここで、 は入射、反射、透過波の波数ベクトルの単位ベクトル、である。 入射波 屈折波 反射波 Maxwellの境界条件( )は境界面に垂直な単位ベクトルとする。 ① ② ③ ④ (a) は常にと垂直(S偏光) ① は自動

Fdtd法の解説ページをリニューアルしました 株式会社科学技術研究所
電磁波 境界条件
電磁波 境界条件-電磁気学Ⅱ Electromagnetics Ⅱ 6/5講義分 電磁波の反射と透過 山田 博仁 * * * * * * * * * * * * * * * * * 界面 e1 e2 異なる媒質の界面における境界条件 53 (教科書p64) の復習 誘電率 e1, e2 の異なる媒質が接している界面 電場に関するGaussの法則を、界面に 存在する高さが無限小の円柱に適用 D1 D2 S 上式吸収境界条件 (Absorbing boundary condition;



Kagawa Nct Ac Jp
電磁波による地下計測技術 第5章 電磁波の反射・散乱 54 5 電磁波の反射・透過・散乱 51 電磁界の境界条件 2つの異なる媒質の境界面においても電磁界はMaxwell の方程式で規定される物理的な条件を満足しなけ ればならない。これが電磁界の境界条件である。誘電体の境界条件 v36 Feb21 1 1st Lst 静磁界の 基本方程式 静磁界の 基本方程式 境界条件とは? 異なる媒質どうしの境界面で生じる特別な条件1S D 2 D D t1 D n1 D n2 D2 t2 D n1D n2 = s 0 表面電荷がある場合や 電荷がない場合や の極限では D n 1 = D n 2 1 E n 1 =$ 2 E n2 電束密度の法線成分の連続性 % & D=# 1,µ ' $,µ 2 ' D&dS S =Q= # v dv upper
『電磁気学第2』講義資料No2 電磁波の発生 電荷分布や電流密度を与えると、マックスウエル方程式を解くことにより電磁場を求めることができる。 そして、それらが時間変動すると電磁波が発生する。 1 遅延ポテンシャル電磁気学III 第7講 2 12 jが存在する場合の減衰波解 z方向に伝播する平面電磁波型の解を考える。この平面電磁波の波数ベクトルはk = (0, 0, k z) である。簡単のために、電場Eがx成分Eのみをもち、磁場Bがy成分Bのみをもつ直線偏光 であるとする。電磁気学III 第8講 3 (0) いま入射波の波数ベクトルのx成分はゼロであり、(86)から反射波および透過波の波数ベクトル のx成分はいずれもゼロだから、 (1) となる。したがって入射波、反射波および透過波の磁場成分は以下のようにあたえられる。
電磁波伝搬を解析するときに、銅などの良導体を完全導体壁とすべきか、表面インピーダンス近似した境界条件を使用すべきかが気になった。 よって、完全導体壁と表面 インピーダンス 法を Maxwell 方程式から導出して、その違いを検討したい。※修正点1017 E1cosθ1=E1n, E2cosθ2=E2nなので、正しくはε1E1cosθ1=D1n, ε2E2cosθ2=D2nです。0000 電束密度0354 電束密度に関するガウスの法則0537 電束密度の完全導体中では電磁波は存在できないので,領域iiの総合電界e ii =0となる。式(8)と式(10)および境界条件より, 境界面(x=0面)で電界の接線成分(y成分)が等しいと置くと次式を得る。
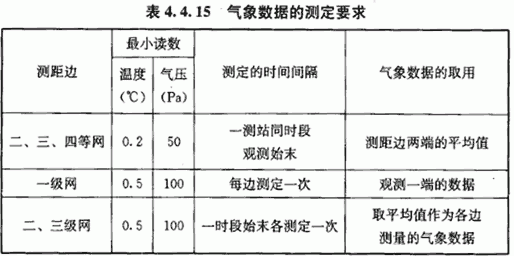



城市测量规范cjjt8 11 筑楼人
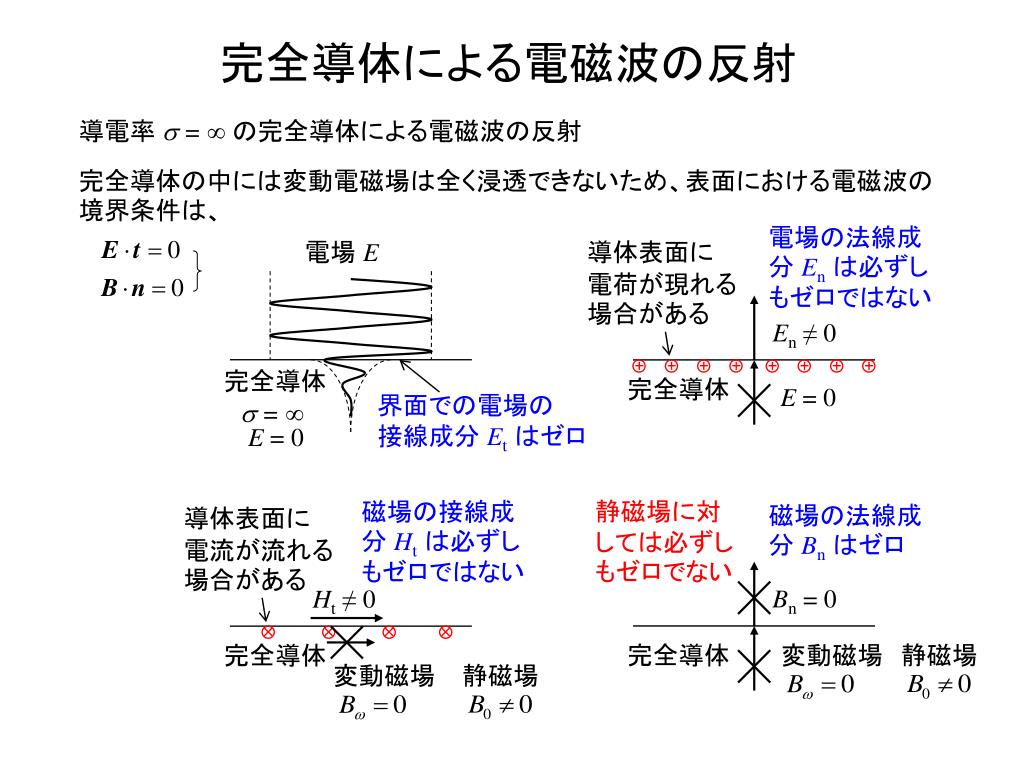



Ppt 電磁気学 C Powerpoint Presentation Free Download Id
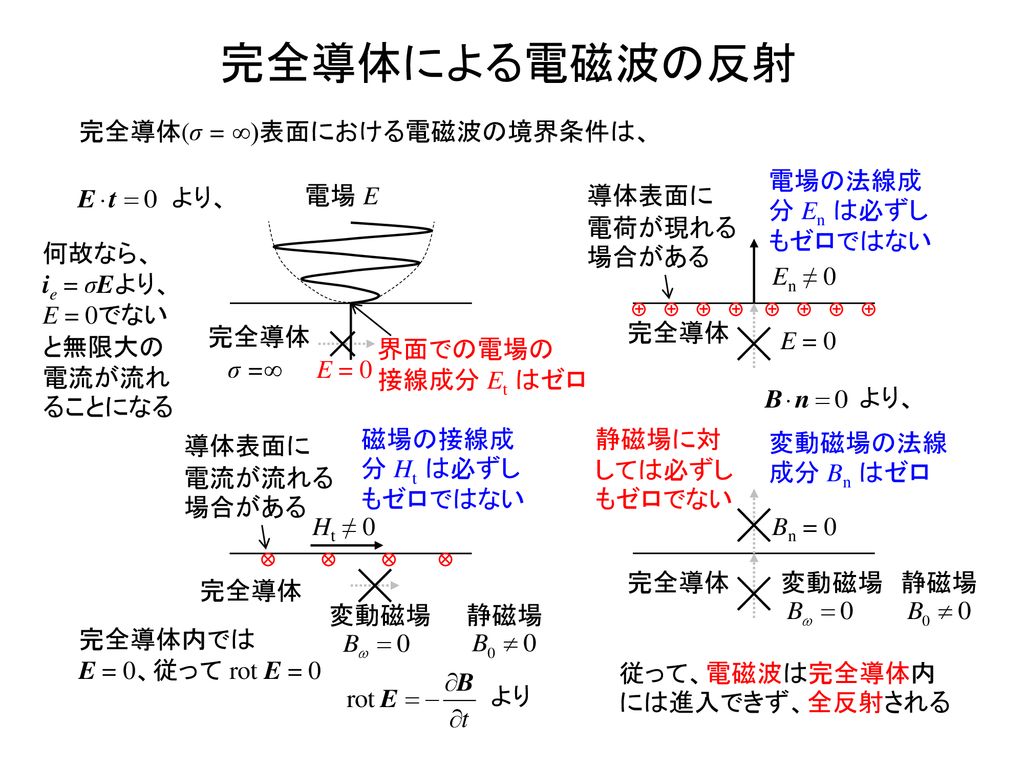
Arial MS Pゴシック MS P明朝 Times New Roman Symbol Wingdings 標準デザイン Microsoft 数式 30 電磁気学Ⅱ 完全導体による電磁波の反射 完全導体による電磁波の反射 完全導体による電磁波の反射 完全導体による電磁波の反射 参考) 伝送線路の場合との比較 波の反射と定在電磁場の異なる物質面における境界条件 物質中のマクスウェル方程式は、形式的には e0 e, m0 m として得られるが、 D (= e E), H (=B/m) と E, B の使い分けに注意する必要がある。 また、物質中の光速度は、 v = w/k = 1/√em である。 境界条件1: E の接線成分が連続 1.不連続面における電磁場の満たすべき境界条件 1 媒体の誘電率や透磁率がある面において不連続に変化する場合で,なおかつ,その不連続面に電荷や電流が存在しないとき,この不連続面における電磁場の境界条件は次のようになります。 (1) 電場 e 、磁場 h (面電流存在しない




逆l形アンテナ アース理論実証 その12 誘電体 5 磁界の強さhの境界条件 Jo3krpの独り言
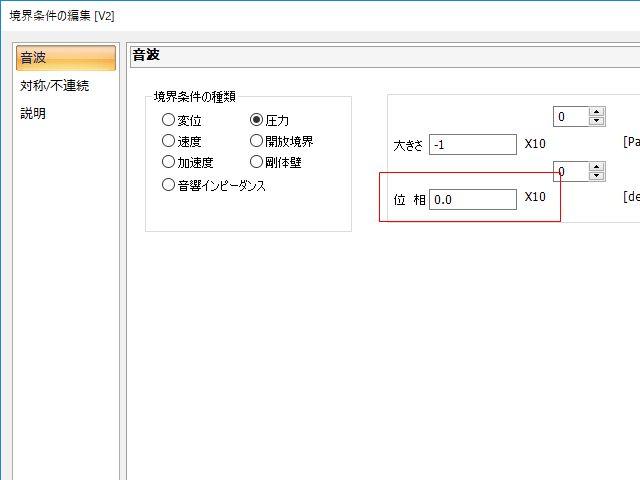



境界条件 ムラタソフトウェアブログ
平面波と境界条件 1 1st Lst v26 Jan21 電磁波における境界条件の使途 Region 1 Region 2 透過 (未知) 111 111 H jE E jH 222 222 H jE E jH 22 EkE1110 22 EkE21 11 1図2 電束密度の法線成分に対する境界条件の計算 導体中電場が存在しない→ 電束密度も存在しな い:領域1を真空、領域2を導体(図2(b)) σn = Dn = ε0En (15) 静電誘導:外部からの電場による導体の表面電荷 の誘起 12 表皮効果 導体中の変動電磁場(図3) rot ・マクスウェル方程式の積分形を使って、電場と磁場の境界条件について考えた。 ・電束密度と磁束密度は法線方向、電場と磁場は接線方向の大きさが、境界面において連続となる。 参考文献 ・伊東敏雄(08)『朝倉物理学選書2 電磁気学』,朝倉書店




Wo19 号 電磁波伝搬制御部材 電磁波伝搬制御構造体 電磁波伝搬制御部材付きサッシ 窓構造体及び電子機器 Astamuse



電磁波の完全導体の境界条件についての質問です 境界面で Yahoo 知恵袋
point 波(電磁波・音波)が,異なる媒質の境界面に対し垂直に入射した場合の反射・透過について. 量子力学で,1次元の階段型ポテンシャルに平面波が入射したときの反射・透過について. これらの波動現象が,ほとんど同じ方法で扱えることを,計算を比較しながら確認する. POINT 散乱問題と同じように,「定常的な状態を扱う方法」と「波を追跡する方法」がある. 前者では「定常的な解+境界条件」をもとに解き,後者は「すべての反射波・透過波(この際,境界条件を考慮)を合成する」ことで解く. 関連記事 層・垂直入射の反射と透過(電磁波境界条件について 異なる媒質の境界(不連続部)では、マクスウェルの方程式はそのまま適用 出来ない。 →境界面に境界条件を適用 媒質内における 電磁波の伝搬 Boundary Plane Medium (ガラスなど) Region1 Region2 Region1 Region2 ε 1 , μ 1 , σ 1 ε 2 , μ 2



光の圧力 輻射圧




電場磁場電磁波 投書 高壓電塔真的會致癌嗎 為 電磁波 闢謠 Ddmba
Minoru TANAKA (Osaka Univ) 25 誘電体の境界条件 • 2種類の誘電体,誘電体1と誘電体2,の境界面を考える.それ ぞれの誘電率をε1,ε2 とし,境界面に電荷はないものとする. 境界面を囲む微小なうすい円筒(底面積 ΔS) を考えて,ガウスの法則を適用すると, (1) D(r)dS =0電磁波工学 柴田幸司 第 6 回 境界条件と伝送線路 伝送線路とは 伝送線路とは光速で進む電磁波を構造体の中に閉じ込めて低損失に波動光学モジュールアップデート COMSOL Multiphysics ® バージョン 54 の波動光学では電磁波 (ビームエンベロープ) インターフェースを使った誘電薄膜計算のための新しい境界条件, 無反射コーティング, 鏡面様表面などの新しいが加わりました 波動光学モジュールのアップデート詳細は以下を
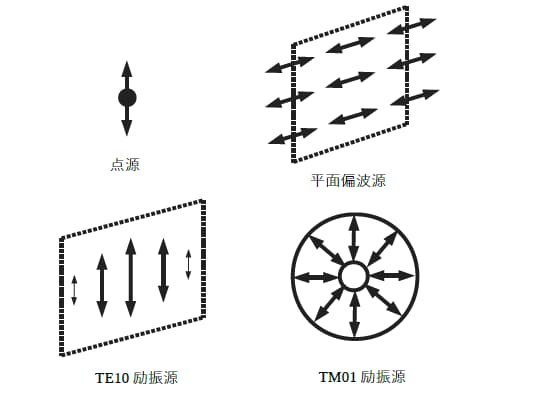



励振源 境界条件 収束判定 解析の実効値 株式会社科学技術研究所




逆l形アンテナ アース理論実証 その13 誘電体 6 電磁波の 電界と磁界の境界条件の関連性 Jo3krpの独り言
電磁気学Ⅱ Electromagnetics Ⅱ 6/5講義分 電磁波の反射と透過 山田 博仁 * * * * * * * * * * * * * * * * * 界面 e1 e2 異なる媒質の界面における境界条件 53 (教科書p64) の復習 誘電率 e1, e2 の異なる媒質が接している界面 電場に関するGaussの法則を、界面に 存在する高さが無限小の円柱に適用 D1 D2 S 上式境界電磁波(光)の反射 電磁波の場合も,音波の圧力波・速度波の関係と同じ事情がある。同じ角振動数ωで振動す る電場ベクトルE と磁場ベクトルH は同位相で,波数ベクトルkに垂直な面内で互いに直交し, (E, H, k)で右手系を成している。このため,例えば垂直入反射を考えると,電場が反射で向き周期境界条件の導入による振幅の規格化 後の計算の便宜のため,周期境界条件を導入し,振幅を規格化する.空間を0 ≤ x ≤ L,0≤ y ≤ L,0≤ z ≤ L の立方体の集まりだと考え,電磁波はこの立方体を周期として周期的になっているとする.L が電磁波の波長よ



2




Pdf 卫星遥感影像处理技术分析
じゃあ実際に電磁界の境界面に平行な成分が連続になるという境界条件を使ってみよう。すると、 \E_{1x}e^{i\omega\left(t\frac{\bar{n}_1}{c}\beta_1 y\right)} E_{1x}'e^{i\omega\left(t\frac{\bar{n}_1}{c}(\alpha_1' x \beta_1' y)\right)} = E_{2x}e^{i\omega\left(t\frac{\bar{n}_2}{c}(\alpha_2 x \beta_2 y)\right)} \tag{1}\ という式が成り立つ 境界条件が成り立つ理由 これらの境界条件がどうやって導かれるかが気になる人もあるだろうし, 全く気にならない人もあるだろう 気にならない人は読み飛ばしてもらっても全く問題ないが, 飛ばし読みするほど難しくもない 第 1 の条件である「境界面に平行な電場成分は連続」の説明電磁界の境界条件により,境界面(y = 0)に対する電界と磁界の接線成分は連続でな ければならない.この場合,接線成分はと成分になるので E i z E r z = E t z , H i x H r x = H t x (15) したがって, e– j k 1 xx R h e – j k x = T h e – j k2 x (16) h – cos θѳ 1 η 1 e



引力与电磁波的爱恨情仇 知乎



2
電磁波には自由空間を伝播する場合や媒質中を伝播する 場合などが考えられるが、この研究では導波管内を伝播す る電磁波について以下のようにまとめる ・Maxwellの方程式 ・二つの異なる媒質の境界での電場、磁場 ・円形導波管内の電磁波 ・まとめ光と色の話 第二部 第1回 光(電磁波ABC) PMLなど (a) 集中ポート (b) 導波路ポート Z 0 V (c) 平面波入射0 ³ */ I 0 V V 0 ³ E d l C I I 0 H d l 入射モード 反射モード 重み 1/2波長以上 散乱体 1/2波ンと呼ぶ.したがって,自由電荷の集団振動が電磁波と結 合した系はプラズモンポラリトンと呼ばれる.表面(また は,境界面)では,固体中でのプラズモンとは状況が異な り,表面での境界条件を満たす別の集団振動が存在するこ




電界と電束密度の境界条件 Cupuasu クプアス



Kagawa Nct Ac Jp
96 第9章 マクスウェルの方程式と電磁波 構成方程式(構成関係式) 物質(誘電体、磁性体)があるとき、以下の関係が成立しますが、これは構成方程 式と呼ばれます。 D(r,t)=ε(r)E(r,t), B(r,t)=μ(r)H(r,t) (95) それ以外の式にローレンツ力などがありますが、ここでは省略します。境界条件 rot t ∂ =− ∂ B E rot t ∂ = ∂ D HJ divB =0 divD =ρ 電磁界に関するすべて の性質はMaxwellの方 程式に記述されている。




電界と電束密度の境界条件 Cupuasu クプアス




電磁気学c Electromagnetics C 5 22講義分 電磁波の反射と透過 山田 博仁 Ppt Download




1998 号 電磁波解析装置及び電磁波解析プログラムを記録したコンピュータ読み取り可能な記録媒体 Astamuse




解析シミュレーションソフトfemtet のバージョンアップについて 村田製作所



员工健康指南
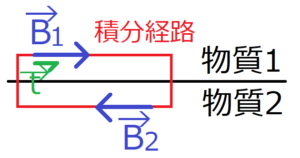



電場と磁場の境界条件



了不起的物理 下载在线阅读书评




战场伪装加重 战争迷雾




最速电磁波能量公式




完全導体境界条件 Ykondo813 S Diary 旧パワエレ Emc日記
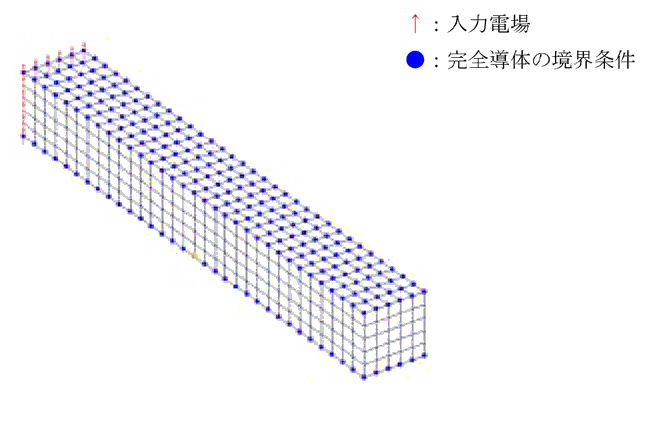



スライドインタフェースを用いた平行平板内の電磁波解析 株式会社フォトン



電磁気の境界条件 の問題について質問です 画像の問題で 電場と電束 Yahoo 知恵袋



2




電場磁場方向 電與磁 Hfep




電磁気学 Electromagnetics 6 30講義分 電磁波の反射と透過 山田 博仁 Ppt Download




新加坡慧灯禅修班 Berichten Facebook




境界条件 ムラタソフトウェアブログ



光の圧力 輻射圧
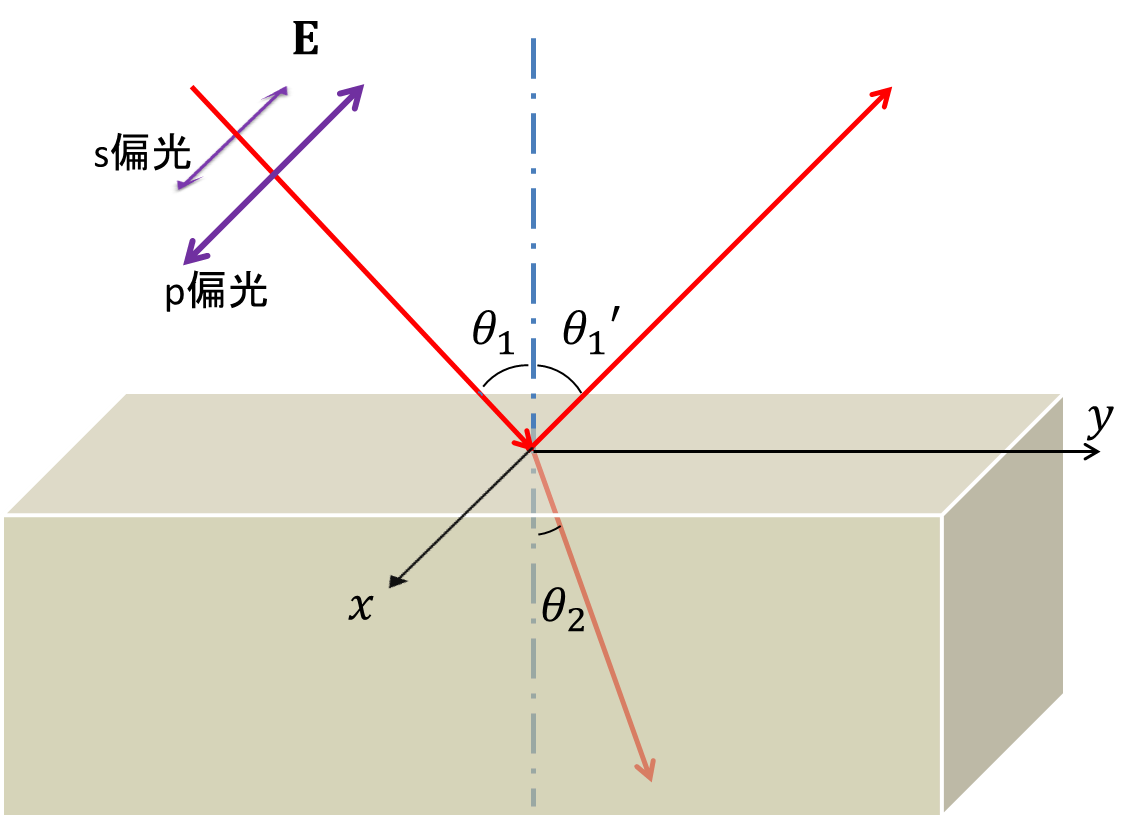



物理とか 偏光と境界条件 反射 屈折の法則




3層 垂直入射の反射と透過 電磁波 音波 Notes Jp




電場磁場方向 電與磁 Hfep
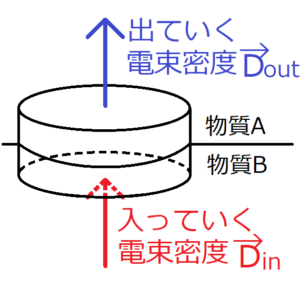



電場と磁場の境界条件



基于环境电磁波的无线传感器节点供电设计2 电子工程世界



2




Woa1 Complex Permittivity Measurement Device Complex Permittivity Measurement Method And Program Google Patents
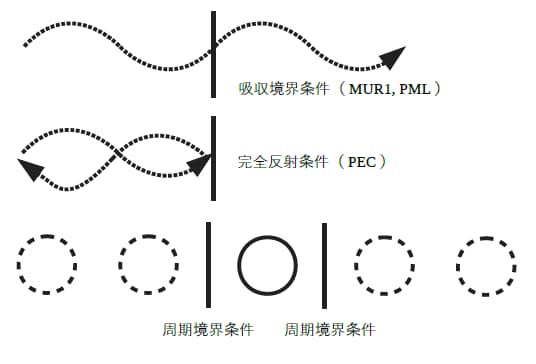



励振源 境界条件 収束判定 解析の実効値 株式会社科学技術研究所
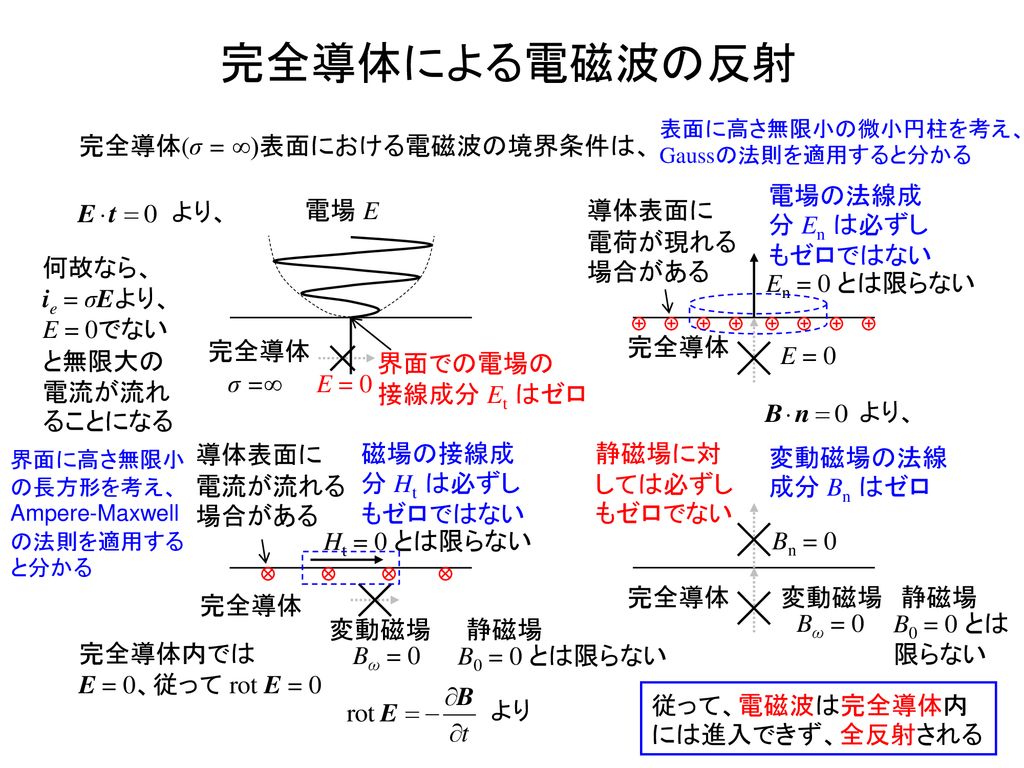



電磁気学 Electromagnetics 6 講義分 共振器と導波路 山田 博仁 Ppt Download



高端窗膜制造的三种 神 器 自由微信 Freewechat




Woa1 Method For Designing Gradient Index Lens And Antenna Device Using Same Google Patents
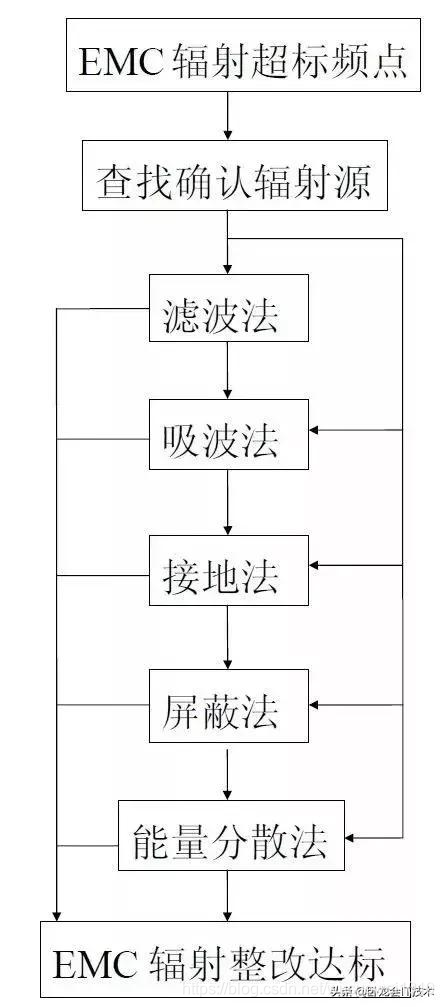



大佬总结的电磁兼容知识 Emc整改六步走 看完感觉太简单了点 Wusuowei1010的博客 程序员宅基地 程序员宅基地



电磁场下载 Ppt模板 爱问共享资料




英国伦敦医美科普 逆龄黑科技超声刀vs热玛吉无创抗衰到底选谁 Ai Beauty 英国伦敦医美整形机构




上海迎华电子科技有限公司



风水太极场



Kyoritsu Pub Co Jp
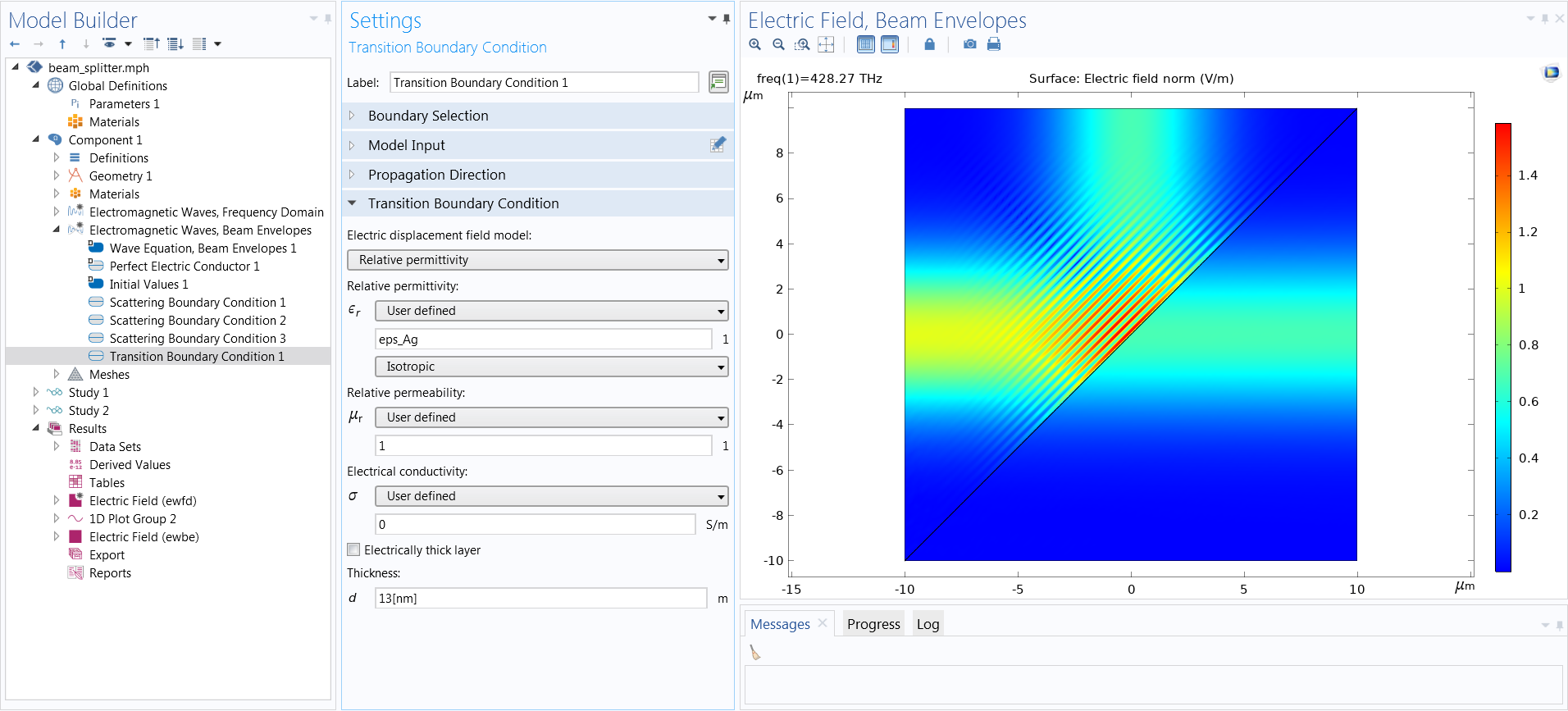



Wave Optics Module Updates Comsol 5 4 Release Highlights



电磁兼容设计中的滤波器 全网搜




電磁気学79 磁束密度と磁界の境界条件とは Youtube



电磁兼容设计中的滤波器 全网搜
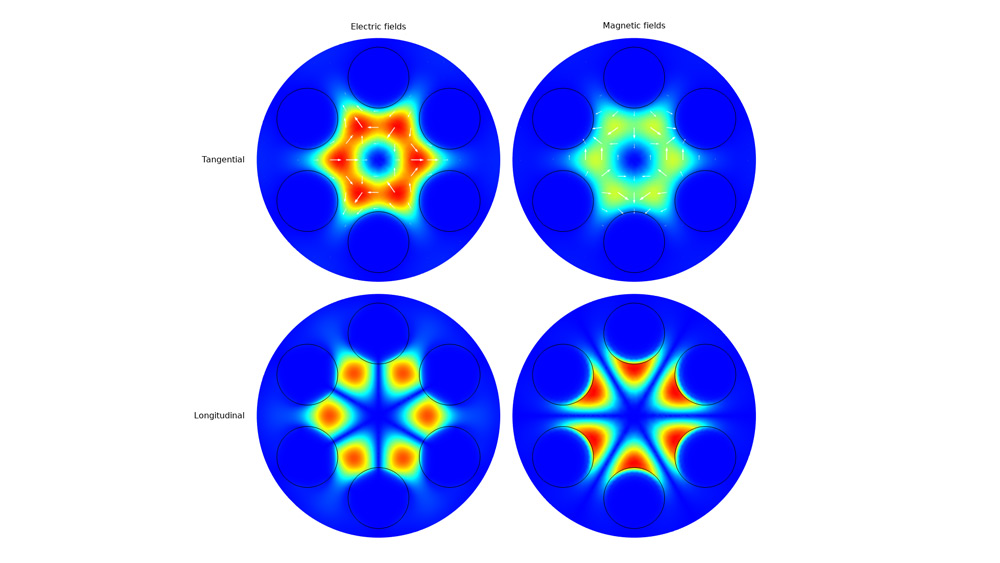



Wave Optics Module Updates Comsol 5 6 Release Highlights



電磁気の境界条件 の問題について質問です 画像の問題で 電場と電束 Yahoo 知恵袋




城市测量规范cjjt8 11 筑楼人




付先生的blog



最速电磁波能量公式
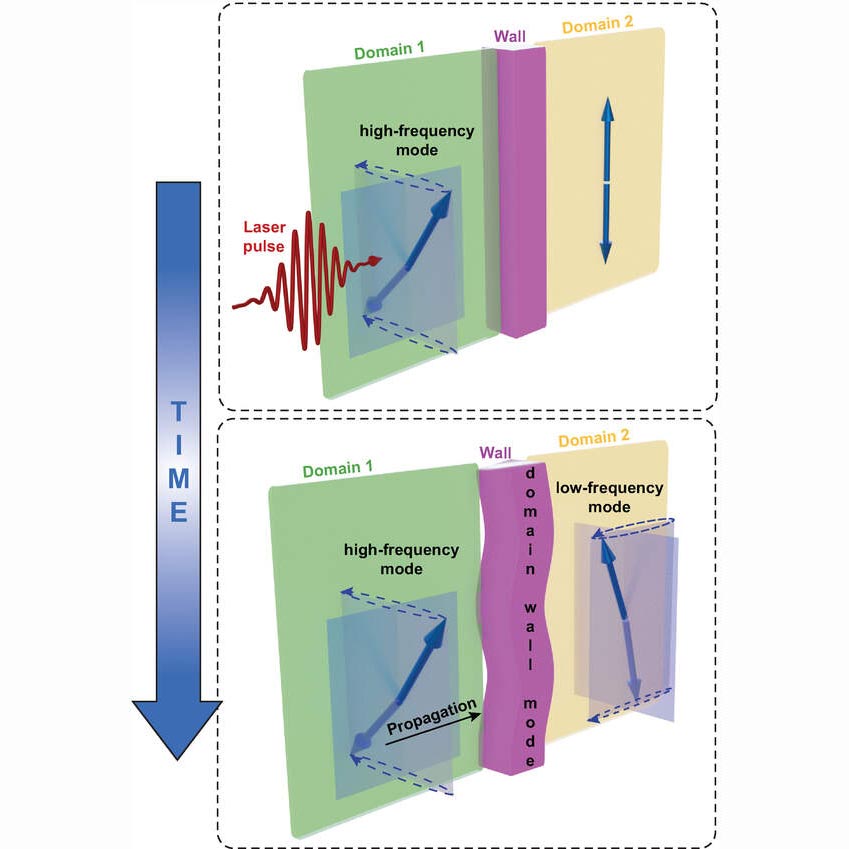



磁现象发现铺平了更快 更高效的数据存储方式 Yabo8



異なる媒質の境界における電磁波と電子波 2 2 電磁波に対する透過係数と反射係数の導出




Woa1 Method For Designing Gradient Index Lens And Antenna Device Using Same Google Patents




乘风破浪的5g 与隐藏在深海的emc暗礁 凤凰网




最速电磁波能量公式




05 号 電磁界解析装置 電磁界解析方法および電磁界解析プログラム Astamuse
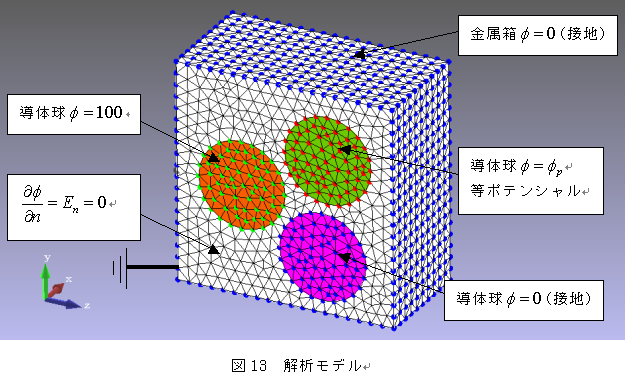



その12 電磁場の境界条件について 株式会社フォトン




18高考物理大一轮复习第14章机械振动机械波光电磁波与相对论第4节光的波动性电磁波相对论课时规范训练下载 Word模板 爱问共享资料




新鮮な電磁波 境界 条件 最高の花の画像
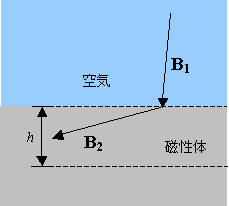



電磁気学における磁性体の境界条件1



Fireinput Wubi86 Table At Master Ollyja Fireinput Github



悟空问答 磁铁的磁力线是由什么构成的 为什么切割磁力线能产生电 力学nerd王小胖的回答 0赞



Kusamalab Org




電場磁場電磁波 投書 高壓電塔真的會致癌嗎 為 電磁波 闢謠 Ddmba



2



9章 反射と屈折の法則



引力与电磁波的爱恨情仇 知乎



Ad 2se Hi Fi 功放 Hi Fi 产品 天逸音响




Wo19 号 電磁波伝搬制御部材 電磁波伝搬制御構造体 電磁波伝搬制御部材付きサッシ 窓構造体及び電子機器 Astamuse




スライドインタフェースを用いた導波管の電磁波解析 株式会社フォトン




波動光学モジュール Comsol 5 1 リリースハイライト



买多优选医之本吸地气少生病理疗鞋的原理是什么 价格多少钱 线上江南




Fdtd法によるアンテナ 電磁波解析 出版物 Tech Seminar Jp



买多优选医之本吸地气少生病理疗鞋的原理是什么 价格多少钱 南方科技网



Uywnvw5o7bou6m




Fdtd法の解説ページをリニューアルしました 株式会社科学技術研究所



2




Sf6断路器辐射电磁波检测技术马宏明 马仪 王伟 何顺 摘要书评试读 京东图书
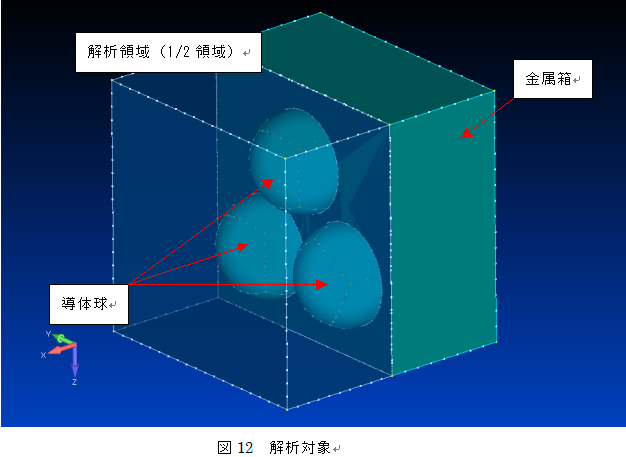



その12 電磁場の境界条件について 株式会社フォトン




最速电磁波能量公式
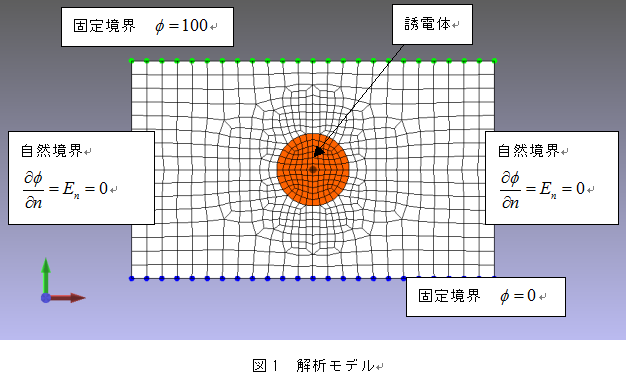



その12 電磁場の境界条件について 株式会社フォトン



2




Woa1 Complex Permittivity Measurement Device Complex Permittivity Measurement Method And Program Google Patents
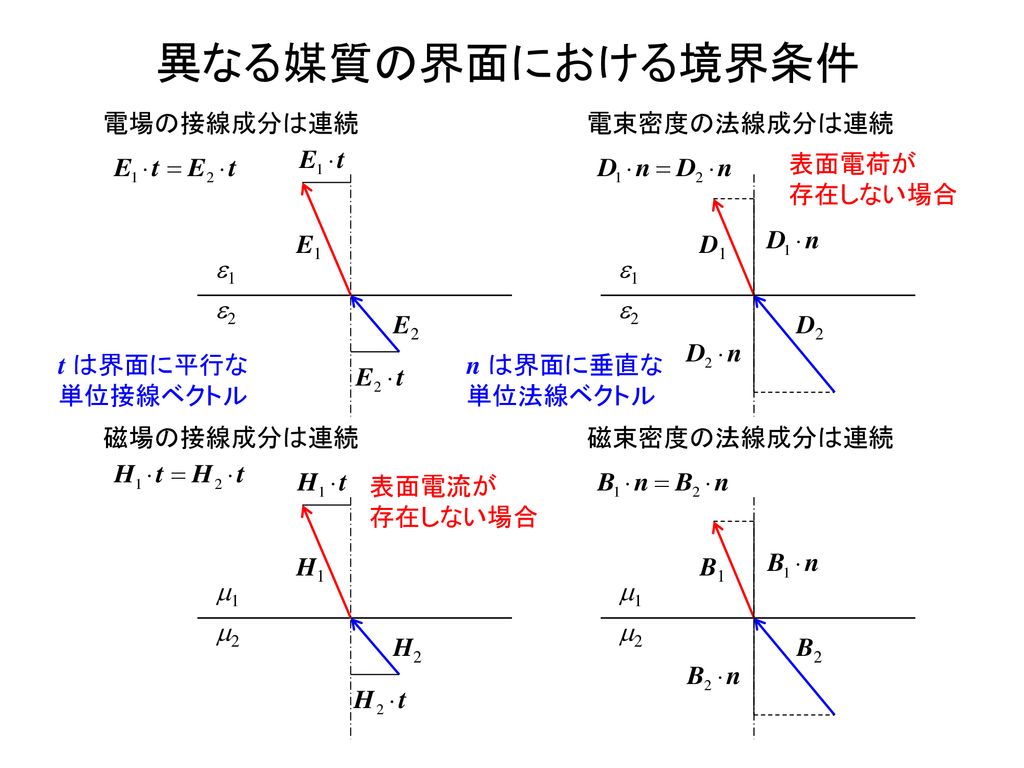



電磁気学 Electromagnetics 6 30講義分 電磁波の反射と透過 山田 博仁 Ppt Download



引力与电磁波的爱恨情仇 知乎




最速电磁波能量公式



引力与电磁波的爱恨情仇 知乎




Matlab电磁场 电磁场与波电磁材料及matlab计算 Sonic Lab的博客 程序员宝宝 程序员宝宝




英国伦敦医美科普 逆龄黑科技超声刀vs热玛吉无创抗衰到底选谁 Ai Beauty 英国伦敦医美整形机构



電磁気学c Electromagnetics C 6 24講義分 共振器と導波路 山田 博仁 Ppt Download



0 件のコメント:
コメントを投稿